Объёмные (3D) элементы

В программе реализованы 2 основных типа объёмных конечных элементов -8-узловой гексаэдр (3D8) и 20-узловой гексаэдр (3D20).

Базовым объёмным конечным элементом является 8-узловой гексаэдр (а), который может вырождаться в любой элемент с меньшим числом узлов до тетраэдра (8,7,6,5,4). Для этого элемента реализованы все возможности, в том числе нелинейное поведение материала вплоть до разрушения, описание свойств жидкости и грунта.

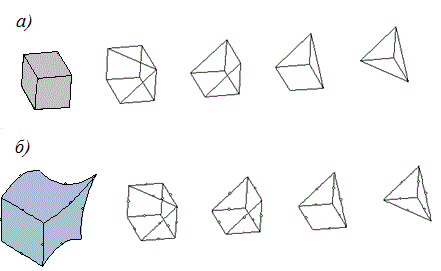
Ограничением для 20-узлового элемента (б) являются возможность описания только линейного поведения материала. Этот элемент также может вырождаться в элемент с меньшим числом узлов (20-4).

Основным отличием элементов является изопараметрия, т.е. независимость свойств элементов от соотношения его сторон. Эти свойства проиллюстрированы на простейшем примере изгиба консольной балки.

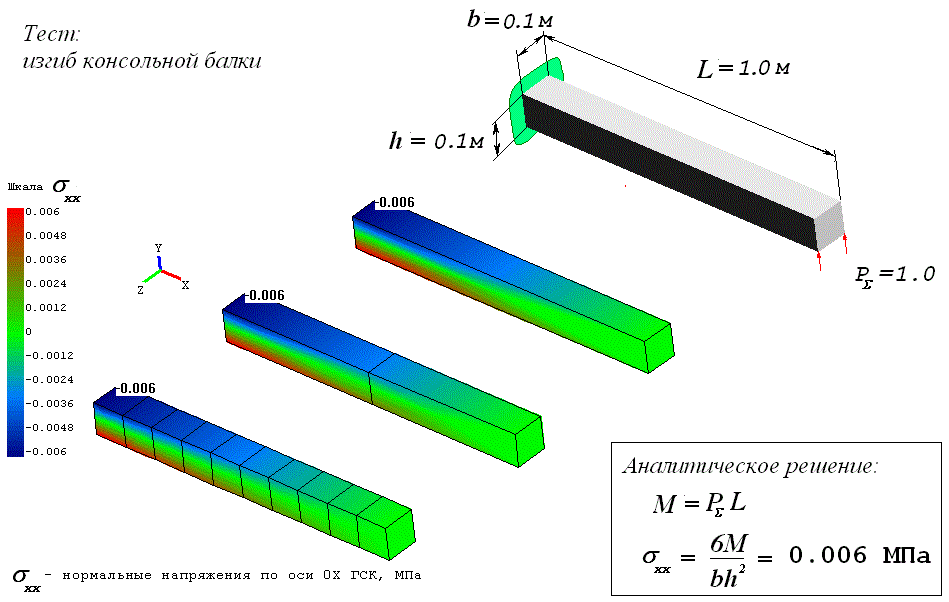
Из представленных данных видно, что значение напряжений, соответствующее аналитическому решению по напряжениям достигается на одном элементе по длине балки. По перемещениям зависимость, всё-таки имеет место. Погрешность по перемещениям на одном элементе составляет -21%, при разбиении балки на два элемента -6,5, далее менее 0,5%. Эти свойства элементов позволяют на грубых сетках получать хорошие приближения параметров напряжённо-деформированного состояния. Свойства достигнуты путём подбора функций формы элемента, способов интегрирования по его объёму, а также способами определения напряжений в элементах. Здесь напряжения можно вычислить как традиционным способом (в точках интегрирования), так и предложенным, новым способом, основанным на анализе равновесия элемента на рёбрах и гранях.

Важным отличием элементов является возможность моделирования больших перемещений. Для иллюстрации этого свойства ниже представлены результаты решения задачи динамики двухстепенного гироскопа, модель которого составлена из объёмных конечных элементов (гексаэдров). Гироскоп, свободно вращающийся c вокруг лежащей в плоскости XOZ собственной оси, через шарниры соединён с вилкой, которой в виде кинематического возмущения задана постоянная скорость вращения вокруг оси OY. Свободное вращение самого гироскопа задано в виде начальных скоростей его узловых точек, соответствующих его вращению как твёрдого тела. Конкретные размеры модели также представлены на рисунке.

На поз. г и д рисунка представлены графики реакций в закреплённых узлах в направлении оси OX. Для обеспечения возможности корректного сравнения параметров, получаемых аналитически методами теоретической механики, значения угловых скоростей и и выбирались такими, чтобы упругие деформации элементов были пренебрежимо малы. При таком движении гироскопа возникает гироскопический момент M , величина которого определяется по теореме Резаля , где Jp - момент инерции гироскопа при вращении вокруг собственной оси. При выбранной расчётной схеме гироскопический момент должен уравновешиваться реакциями в закреплениях, действующими в плоскости XOZ. При этом максимальная величина реакции Pmax в направлении координатной оси будет в момент, когда ось вращения гироскопа параллельна выбранной оси системы координат.

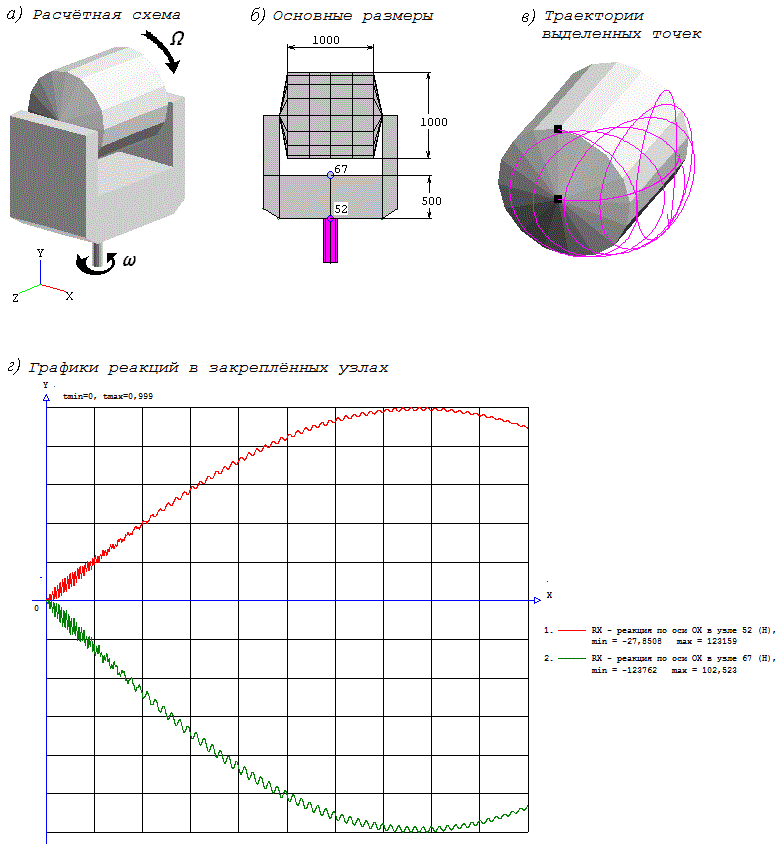
Из графиков, представленных на рисунке, видно, что максимальные по амплитуде значения реакций в направлении оси OX имеют место, когда ось вращения гироскопа становится параллельной указанной оси. Погрешность получаемых значений реакций определится выражением =(Pa -Pmax)/ Pa , где Pa = M / L-значение реакции, получаемое из аналитического решения, где L -расстояние между точками закрепления. В таблице 1 приведены значения (%) для моделей гироскопа из N элементов, полученные при значениях (определяется по модели гироскопа), L =500 мм, = 2 рад/с и = 40 рад/с. Для заданных значений параметров максимальная величина реакции в закреплённом узле Pa = 125360 Н. Из графиков, представленных на рисунке видно, что полученные из численного решения величины реакций имеют значения 123762,0 Н и 123159,0 Н, соответственно погрешность равна 1,51%. Представленные результаты получены при интегрировании по времени с шагом 0.0002с. Уменьшая шаг интегрирования по времени можно добиться ещё меньшей погрешности.